نحوه محاسبه توان برق به زبان ساده

توان الکتریکی در مدارهای AC و DC

توان الکتریکی یکی از مفاهیم اساسی در الکترونیک و مهندسی برق است که به میزان انرژی منتقل‌شده یا مصرف‌شده توسط دستگاه‌های الکتریکی در واحد زمان اشاره دارد. توان در مدارهای جریان مستقیم (DC) و جریان متناوب (AC) محاسبه می‌شود، اما فرمول‌ها و مفاهیم آن‌ها در این دو نوع مدار متفاوت است. در این مقاله، به بررسی نحوه محاسبه توان در هر دو نوع مدار AC و DC پرداخته می‌شود.

۱. توان در مدارهای DC

در مدارهای جریان مستقیم (DC)، جریان الکتریکی در یک جهت ثابت جریان دارد. در این نوع مدار، ولتاژ و جریان نیز ثابت هستند. بنابراین، توان الکتریکی در مدار DC نسبت به مدار AC نسبتاً ساده‌تر محاسبه می‌شود.

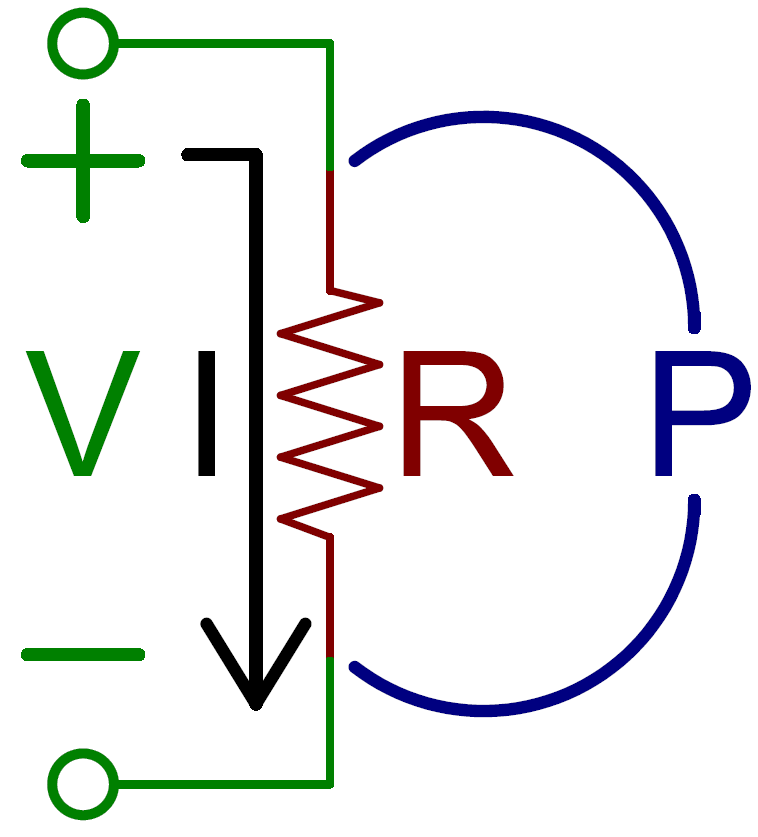
فرمول محاسبه توان در مدار DC: P=V×IP = V \times IP=V×I

که در آن:

• PPP توان الکتریکی (در واحد وات)
• VVV ولتاژ (در واحد ولت)
• III جریان (در واحد آمپر)

در این حالت، توان به طور مستقیم به ولتاژ و جریان بستگی دارد و معمولاً ثابت است. به عنوان مثال، اگر ولتاژ یک باتری 12 ولت باشد و جریان 2 آمپر از آن عبور کند، توان مصرفی به این صورت محاسبه می‌شود: P=12 V×2 A=24 واتP = 12 \, \text{V} \times 2 \, \text{A} = 24 \, \text{وات}P=12V×2A=24وات

این توان به طور ثابت در مدار جاری خواهد بود.

۲. توان در مدارهای AC

در مدارهای جریان متناوب (AC)، ولتاژ و جریان به صورت متناوب تغییر می‌کنند. این بدان معنی است که ولتاژ و جریان در هر دوره زمانی تغییر جهت داده و شدت آن‌ها تغییر می‌کند. در نتیجه، محاسبه توان در مدارهای AC پیچیده‌تر از مدارهای DC است. در مدارهای AC باید دو نوع توان مختلف را در نظر بگیریم: توان واقعی (P) و توان ظاهری (S).

۲.۱. توان واقعی (Real Power) یا توان اکتیو (P)

توان واقعی یا توان اکتیو همان توانی است که واقعاً در یک بار مصرف می‌شود و در واحد وات (W) اندازه‌گیری می‌شود. در مدارهای AC، توان واقعی به‌طور مستقیم به مولفه‌های ولتاژ و جریان که با یکدیگر هم‌فاز هستند، بستگی دارد. توان واقعی معمولاً با فرمول زیر محاسبه می‌شود: P=Vrms×Irms×cos⁡(θ)P = V_{\text{rms}} \times I_{\text{rms}} \times \cos(\theta)P=Vrms​×Irms​×cos(θ)

که در آن:

• PPP توان واقعی (وات)
• VrmsV_{\text{rms}}Vrms​ ولتاژ موثر (ریشه میانگین مربع) (ولتاژ AC)
• IrmsI_{\text{rms}}Irms​ جریان موثر (آمپر)
• θ\thetaθ زاویه فاز بین ولتاژ و جریان

در اینجا، cos⁡(θ)\cos(\theta)cos(θ) که به آن ضریب توان (Power Factor) می‌گویند، نشان‌دهنده نسبت توان واقعی به توان ظاهری است و معمولاً مقداری بین 0 و 1 دارد.

۲.۲. توان ظاهری (Apparent Power) یا توان کاذب (S)

توان ظاهری مجموع توان واقعی و توان راکتیو است که در واحد ولت-آمپر (VA) اندازه‌گیری می‌شود. در مدارهای AC، توان ظاهری به‌طور کلی با استفاده از فرمول زیر محاسبه می‌شود: S=Vrms×IrmsS = V_{\text{rms}} \times I_{\text{rms}}S=Vrms​×Irms​

توان ظاهری در واقع توان کل منتقل‌شده در مدار است، بدون توجه به اینکه این توان در نهایت به کار مفید تبدیل می‌شود یا به صورت انرژی راکتیو به سیستم باز می‌گردد.

۲.۳. توان راکتیو (Reactive Power) یا توان القایی (Q)

توان راکتیو همانطور که از نامش پیداست به‌طور مستقیم با عناصر راکتیو مانند سلف و خازن در مدارهای AC مرتبط است. این توان در نهایت هیچ‌گونه کار مفیدی انجام نمی‌دهد، اما در سیستم جریان می‌یابد و در لحظاتی ذخیره و در لحظات دیگر آزاد می‌شود. فرمول محاسبه توان راکتیو به شکل زیر است: Q=Vrms×Irms×sin⁡(θ)Q = V_{\text{rms}} \times I_{\text{rms}} \times \sin(\theta)Q=Vrms​×Irms​×sin(θ)

توان راکتیو در واحد ولت-آمپر راکتیو (VAR) اندازه‌گیری می‌شود و به دو دسته تقسیم می‌شود: توان راکتیو القایی (که توسط سلف‌ها تولید می‌شود) و توان راکتیو خازنی (که توسط خازن‌ها تولید می‌شود).

۲.۴. رابطه میان توان واقعی، توان ظاهری و توان راکتیو

توان واقعی، توان ظاهری و توان راکتیو ارتباط نزدیکی با یکدیگر دارند و می‌توان آن‌ها را به‌صورت مثلث توان نشان داد. این سه نوع توان با هم به صورت زیر مرتبط هستند: S2=P2+Q2S^2 = P^2 + Q^2S2=P2+Q2

در اینجا، PPP توان واقعی، QQQ توان راکتیو و SSS توان ظاهری است.

۳. مثال از توان در مدارهای AC

فرض کنید یک موتور الکتریکی در مدار AC با ولتاژ 220 V220 \, \text{V}220V و جریان 5 A5 \, \text{A}5A کار می‌کند. همچنین فرض کنید ضریب توان cos⁡(θ)=0.8\cos(\theta) = 0.8cos(θ)=0.8 باشد.

برای محاسبه توان واقعی: P=220 V×5 A×0.8=880 واتP = 220 \, \text{V} \times 5 \, \text{A} \times 0.8 = 880 \, \text{وات}P=220V×5A×0.8=880وات

برای محاسبه توان ظاهری: S=220 V×5 A=1100 ولت-آمپرS = 220 \, \text{V} \times 5 \, \text{A} = 1100 \, \text{ولت-آمپر}S=220V×5A=1100ولت-آمپر

و برای محاسبه توان راکتیو: Q=220 V×5 A×sin⁡(θ)Q = 220 \, \text{V} \times 5 \, \text{A} \times \sin(\theta)Q=220V×5A×sin(θ)

چون cos⁡(θ)=0.8\cos(\theta) = 0.8cos(θ)=0.8، می‌توان از رابطه sin⁡(θ)=1−cos⁡2(θ)\sin(\theta) = \sqrt{1 – \cos^2(\theta)}sin(θ)=1−cos2(θ)​ استفاده کرد: sin⁡(θ)=1−0.82=0.6\sin(\theta) = \sqrt{1 – 0.8^2} = 0.6sin(θ)=1−0.82​=0.6

بنابراین: Q=220 V×5 A×0.6=660 ولت-آمپر راکتیوQ = 220 \, \text{V} \times 5 \, \text{A} \times 0.6 = 660 \, \text{ولت-آمپر راکتیو}Q=220V×5A×0.6=660ولت-آمپر راکتیو

۴. نتیجه‌گیری

در مدارهای DC، توان الکتریکی به سادگی از حاصل‌ضرب ولتاژ و جریان محاسبه می‌شود و به صورت ثابت باقی می‌ماند. اما در مدارهای AC، به دلیل تغییرات دوره‌ای ولتاژ و جریان، توان به سه بخش واقعی، ظاهری و راکتیو تقسیم می‌شود. توان واقعی همان توان مفیدی است که در مدار مصرف می‌شود، در حالی که توان ظاهری مجموع توان واقعی و راکتیو است و توان راکتیو در واقع برای نگهداری میدان‌های مغناطیسی و الکتریکی در مدار مصرف می‌شود اما در نهایت به کار مفید تبدیل نمی‌شود.

با درک این مفاهیم، می‌توان عملکرد و بهره‌وری سیستم‌های الکتریکی را به‌طور مؤثرتری مدیریت کرد.

معادله معروف نسبیت: $ E = mc^2 $

فرمول انرژی در فیزیک: